纺锤体和纺锤丝

$n$ 个点 $m$ 条边的图。判断是否图中每个简单环长度都相同。

$n,m\le 5\times 10^5$ 。

对于每个点双单独考虑。

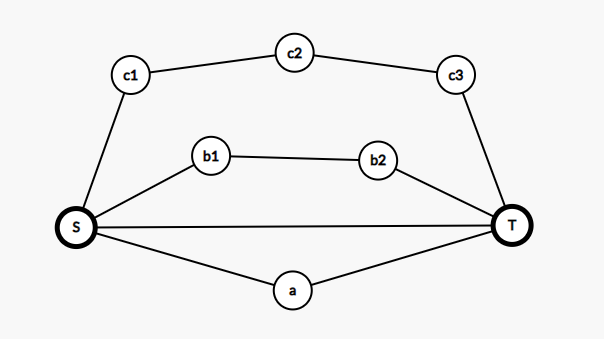
合法情况形如两个端点和若干条链。形似纺锤体和纺锤丝。

要说明在此基础上加任意一条边都非法。加的边的端点可以在同一条链上或在两条链上，都会推出必须存在边权为 $0$ 的边，退化后还是形如这样的结构。

int n,m,ans,fl;
pii edge[maxn];
vector<int> e[maxn],g[maxn];
int dfn[maxn],lw[maxn],idx;
int st[maxn],tp;
int scc[maxn],scct;
int dep[maxn];
void tar(int u){
	dfn[u]=lw[u]=++idx;st[++tp]=u;
	for(int v:e[u]){
		if(!dfn[v]){
			dep[v]=dep[u]+1;tar(v);
			lw[u]=min(lw[u],lw[v]);
			if(lw[v]>=dfn[u]){
				++scct;
				g[scct].pb(st[tp]);
				while(st[tp--]!=v)g[scct].pb(st[tp]);
				g[scct].pb(u);
			}
		}
		else lw[u]=min(lw[u],dfn[v]);
	}
}
vector<pii> ee[maxn];
bool vis[maxn];
void dfs(int u,int fa){
	vis[u]=1;dep[u]=dep[fa]+1;
	for(int v:e[u])if(v!=fa){
		if(!vis[v])dfs(v,u);
	}
}
int d[maxn];
void work(){
	n=read();m=read();ans=-1;fl=0;
	for(int i=1;i<=n;i++)e[i].clear(),g[i].clear();
	for(int i=1;i<=n;i++)dfn[i]=dep[i]=0;idx=tp=scct=0;
	for(int i=1;i<=m;i++){
		int u=read(),v=read();
		e[u].pb(v),e[v].pb(u);
	}
	tar(1);
	for(int i=1;i<=scct;i++){
		sort(g[i].begin(),g[i].end(),[&](int u,int v){return dep[u]<dep[v];});
		for(int j=1;j<g[i].size();j++)scc[g[i][j]]=i;
		ee[i].clear();
	}
	for(int u=1;u<=n;u++){
		for(int v:e[u])if(dep[u]<dep[v]||(dep[u]==dep[v]&&u<v))ee[scc[v]].pb({u,v});
	}
	for(int i=1;i<=scct;i++)if(g[i].size()>2){
		for(int u:g[i])e[u].clear(),vis[u]=0,d[u]=0;
		for(auto[u,v]:ee[i])d[u]++,d[v]++,e[u].pb(v),e[v].pb(u);
		int num=0;for(int u:g[i])num+=(d[u]==2);
		if(num==g[i].size()){
			if(ans==-1)ans=num;
			else if(ans!=num)fl=1;
		}
        else if(num+2==g[i].size()){
			int p1=0,p2=0;
			for(int u:g[i])if(d[u]!=2)(!p1?p1:p2)=u;
			vis[p2]=1;dfs(p1,0);
			for(int v:e[p2]){
				if(ans==-1)ans=dep[v]*2;
				else if(ans!=dep[v]*2)fl=1;
			}
		}
        else fl=1;
	}
	if(fl)puts("No");
	else puts("Yes");
}

P8331

$n$ 个点 $m$ 条带权边的图。保证存在重新赋正边权的方案使得图中每个简单环边权和都相同。

$q$ 次询问 $u\to v$ 的所有简单路径权值和。

$n,m,q\le 5\times 10^5$ 。

对每个点双找到上述纺锤体和纺锤丝结构后，可以 $O(1)$ 处理一个点双内两个点的所有简单路径数和所有简单路径权值和，记为 $(num,sum)$ 。

记 $cnt$ 为纺锤丝数， $all$ 为整个点双的边权和。如果 $u,v$ 在同一条链上， $A,B$ 为两个纺锤体， $u$ 更靠近 $A$ ， $(num,sum)=(cnt,all+(cnt-2)(dis(A,u)+dis(B,v)))$ 。否则 $(num,sum)=2(cnt-1),2all+(cnt-3)(dis(A,u)+dis(B,u)+dis(A,v)+dis(B,v))$ 。

建圆方树， $u\to v$ 路径上的圆点都是必经点，倍增在一级祖先（方点）的点双内，圆点 $u$ 去到二级祖先（圆点）的二元组。每次询问如果 lca 为方点，在额外计算 lca（方点）的点双内，两个圆点的二元组。

复杂度 $O(n\log n)$ 。

int n,m,q;
vector<pii> e[maxn];
vector<int> g[maxn];
int dfn[maxn],lw[maxn],idx;
int st[maxn],tp;
int scc[maxn],scct;
int dep[maxn];
void tar(int u){
	dfn[u]=lw[u]=++idx;st[++tp]=u;
	for(auto[v,w]:e[u]){
		if(!dfn[v]){
			dep[v]=dep[u]+1;tar(v);
			lw[u]=min(lw[u],lw[v]);
			if(lw[v]>=dfn[u]){
				++scct;
				g[scct].pb(st[tp]),g[st[tp]].pb(scct);
				while(st[tp--]!=v)g[scct].pb(st[tp]),g[st[tp]].pb(scct);
				g[scct].pb(u),g[u].pb(scct);
			}
		}
		else lw[u]=min(lw[u],dfn[v]);
	}
}
vector<tuple<int,int,int>> ee[maxn];
pii merge(pii u,pii v){return {u.fi*v.fi%mod,(u.fi*v.se+u.se*v.fi)%mod};}
int to[maxn][20];
pii val[maxn][20];
int a[maxn],b[maxn],num[maxn],sum[maxn];
vector<int> d[maxn],disa[maxn],disb[maxn],pos[maxn];
int rnk[maxn];
void dfsa(int id,int u,int fa){
	for(auto[v,w]:e[u])if(v!=fa){
		if(v==g[id][b[id]])continue;
		disa[id][rnk[v]]=disa[id][rnk[u]]+w;
		dfsa(id,v,u);
	}
}
void dfsb(int id,int u,int fa){
	for(auto[v,w]:e[u])if(v!=fa){
		if(v==g[id][a[id]])continue;
		disb[id][rnk[v]]=disb[id][rnk[u]]+w;
		dfsb(id,v,u);
	}
}
void dfsp(int id,int u,int fa,int fr){
	pos[id][rnk[u]]=fr;
	for(auto[v,w]:e[u])if(v!=fa){
		if(v==g[id][b[id]])continue;
		dfsp(id,v,u,fr);
	}
}
void init(int id){
	int sz=g[id].size();
	sort(g[id].begin(),g[id].end());
	d[id].resize(sz),disa[id].resize(sz),disb[id].resize(sz),pos[id].resize(sz);
	for(int i=0;i<sz;i++)rnk[g[id][i]]=i;
	for(auto[u,v,w]:ee[id])d[id][rnk[u]]++,d[id][rnk[v]]++;
	a[id]=b[id]=-1;
	for(int i=0;i<sz;i++)if(d[id][i]>2)(a[id]==-1?a[id]:b[id])=i;
	if(a[id]==-1)a[id]=0,b[id]=1;
	for(int u:g[id])e[u].clear();
	for(auto[u,v,w]:ee[id])e[u].pb({v,w}),e[v].pb({u,w}),sum[id]+=w;sum[id]%=mod;
	dfsa(id,g[id][a[id]],0),dfsb(id,g[id][b[id]],0);
	disa[id][b[id]]=disb[id][a[id]]=inf;
	pos[id][a[id]]=-1,pos[id][b[id]]=-1;
	for(auto [v,w]:e[g[id][a[id]]]){
		++num[id];
		if(v==g[id][b[id]])continue;
		dfsp(id,v,g[id][a[id]],num[id]);
	}
}
pii calc(int id,int u,int v){
	int p=lower_bound(g[id].begin(),g[id].end(),u)-g[id].begin();
	int q=lower_bound(g[id].begin(),g[id].end(),v)-g[id].begin();
	if(pos[id][p]!=-1&&pos[id][q]!=-1&&pos[id][p]!=pos[id][q]){
		return {2*(num[id]-1),(2*sum[id]+(disa[id][p]+disb[id][p]+disa[id][q]+disb[id][q])%mod*(num[id]+mod-3))%mod};
	}
	int va=0,vb=0;
	if(disa[id][p]<disa[id][q])va=disa[id][p],vb=disb[id][q];
	else va=disa[id][q],vb=disb[id][p];
	return {num[id],(sum[id]+(va+vb)%mod*(num[id]-2))%mod};
}
void dfs(int u,int fa){
	dep[u]=dep[fa]+1;to[u][0]=fa;
	for(int i=1;i<20;i++)to[u][i]=to[to[u][i-1]][i-1];
	if(u<=n&&u>1)val[u][0]=calc(to[u][0],u,to[u][1]);
	for(int i=1;i<20;i++)val[u][i]=merge(val[u][i-1],val[to[u][i]][i-1]);
	for(int v:g[u])if(v!=fa)dfs(v,u);
}
int lca(int u,int v){
	if(dep[u]<dep[v])swap(u,v);
	for(int i=19;~i;i--)if(dep[to[u][i]]>=dep[v])u=to[u][i];
	if(u==v)return u;
	for(int i=19;~i;i--)if(to[u][i]!=to[v][i])u=to[u][i],v=to[v][i];
	return to[u][0];
}
int que(int u,int v){
	int tp=lca(u,v);
	pii res={1,0};
	for(int i=19;i;i--)if(dep[to[u][i]]>=dep[tp])res=merge(res,val[u][i-1]),u=to[u][i];
	for(int i=19;i;i--)if(dep[to[v][i]]>=dep[tp])res=merge(res,val[v][i-1]),v=to[v][i];
	if(u==v)return res.se;
	return merge(res,calc(to[u][0],u,v)).se;
}
void work(){
	n=read();m=read();q=read();	
	for(int i=1;i<=m;i++){
		int u=read(),v=read(),w=read();
		e[u].pb({v,w}),e[v].pb({u,w});
	}
	scct=n;tar(1);
	for(int i=n+1;i<=scct;i++){
		sort(g[i].begin(),g[i].end(),[&](int u,int v){return dep[u]<dep[v];});
		for(int j=1;j<g[i].size();j++)scc[g[i][j]]=i;
	}
	for(int u=1;u<=n;u++){
		for(auto[v,w]:e[u])if(dep[u]<dep[v]||(dep[u]==dep[v]&&u<v))ee[scc[v]].pb({u,v,w});
	}
	for(int i=n+1;i<=scct;i++)init(i);
	dfs(1,0);
	while(q--){
		int u=read(),v=read();
		write(que(u,v));puts("");
	}
}

感谢您的支持，我会继续努力的!